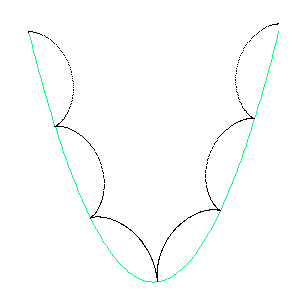
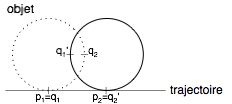
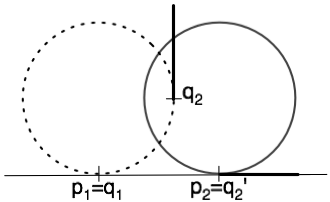
 Quand un objet roule sur une trajectoire d'un point p1 à un point p2, l'objet doit être déplacé et tourné. Au point p1 l'objet touche la trajectoire au point q1. Au point p2 de la trajectoire, le point de contact est devenu le point q2'.
Quand un objet roule sur une trajectoire d'un point p1 à un point p2, l'objet doit être déplacé et tourné. Au point p1 l'objet touche la trajectoire au point q1. Au point p2 de la trajectoire, le point de contact est devenu le point q2'.Objectif: Appliquer les connaissances de C++ acquises.
Le but de cet exercice est de compléter l'infrastructure existante pour permettre la simulation d'une cycloïde ou astroïde en faisant rouler un cercle sur une trajectoire (linéaire ou circulaire).
La cycloïde et l'astroïde tracées lors de l'exercice précédent par des fonctions paramétriques peuvent être engendrées par un point d'un cercle qui roule sur une trajectoire. Pour la cycloïde, cette trajectoire est une droite horizontale. Pour l'astroïde, la trajectoire est elle-même un cercle. Une belle animation de ce qu'on aimerait simuler est disponible sur le site web de Wolfram Research: la cycloïde et l'astroïde.
L'implémentation se fait par petites étapes qui sont en partie données et en partie réalisées par l'étudiant.
La figure suivante montre une vue d'ensemble de la hiérarchie de classes manipulée lors de cet exercice :
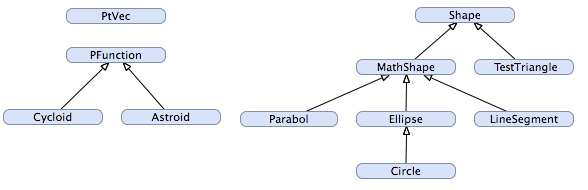
Les résultats des exercices précédents, c'est-à-dire les classes PtVec, PFunction, Cycloid et Astroid, vont être réutilisés. Lors des étapes qui suivent, vous allez implémenter les classes MathShape, TestTriangle, Ellipse et Circle. Toutes les autres classes seront fournies.
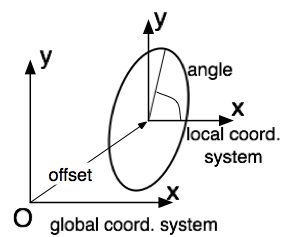
La classe Shape est une classe abstraite qui représente une forme quelconque pouvant être affichée, déplacée et tournée autour d'un centre de rotation. A cette fin, elle stocke les informations suivantes :
offset, c'est-à-dire la position relative du système de coordonées local par rapport à l'origine du système de coordonnées global.centerOfRot en coordonnées locales. En général (0, 0).anglecolorLe code source de cette classe abstraite est le suivant :
(Vous pouvez le copier dans un fichier .cpp)
Une fonction particulière est translateRotatePoint(). Elle applique à un point donné la rotation autour du centre et la translation. Cette fonction utilitaire permet aux sous-classes de ne pas devoir s'occuper de la position et la rotation de la forme. (C'est pour ça qu'on fait des classes, non?)
Manipulation 4.1 (Test de Shape) : Etudiez le fonctionnement de la classe Shape et écrivez une sous-classe TestTriangle qui implémente la méthode draw() pour dessiner un triangle. Utilisez comme points de base du triangle les points (0, 0), (1, 0) et (0.5, 1).
Conseils :
lspxgraph pour gérer la fenêtre et dessiner à l'intérieur.draw() appliquez la fonction translateRotatePoint() à chaque sommet du triangle.activateColor() pour demander à la classe Shape d'activer la couleur de la forme.Question 4.1 : Pourquoi est-il nécessaire d'appliquer la fonction translateRotatePoint() à chaque point de la forme lors de l'exécution de draw()?
Maintenant, nous aimerions implémenter un moyen alternatif de définir des formes. Au lieu d'implémenter la méthode draw() dans toutes les classes de forme, on aimerait définir une forme à partir d'une fonction génératrice f. Comme on aimerait qu'il s'agisse toujours de formes qu'on peut déplacer et tourner à volonté, la classe MathShape hérite de la classe Shape vue dans l'étape précédente.
Une forme mathématique est entièrement définie par une fonction génératrice f et le domaine de définition de la fonction. La fonction f est identique à ce qu'on a vu dans l'exercice précédent sur les fonctions paramétriques. Le domaine de définition définit le domaine dans lequel le paramètre t peut varier, p.ex. [0, 2*PI] pour un cercle.
Manipulation 4.2 : Créez la classe abstraite MathShape. Elle hérite de la classe Shape et a les propriétés et méthodes suivantes :
tmin et tmaxf qui retourne un point de la fonction génératrice pour un paramètre t donné.getDomain() et setDomain() pour lire et modifier le domaine de définition.computePoint() qui calcule à partir d'un paramètre t la position du point de la forme. (=le résultat tient compte de la position courante et la rotation de la forme)draw() dessine la forme (et pas le graphe de la fonction génératrice!) par des segments de droites. tmin et tmaxLa classe MathShape est très similaire à la classe PFunction qui a été créée lors de l'exercice précédent. Vous pouvez donc reprendre une grande partie du code!
Testez votre implémentation avec le programme de test suivant : (classe Parabol et fonction MathShape)
Manipulation 4.3 : Créez des sous-classes Circle et Ellipse qui héritent de MathShape et implémentent un cercle dont le rayon est modifiable et une ellipse dont les demis-axes a et b peuvent être spécifiés.
Conseil : Vous pouvez implémenter le cercle comme cas particulier d'ellipse. La fonction paramétrique de l'ellipse est : x=a*cos(t), y=b*sin(t)
 Quand un objet roule sur une trajectoire d'un point p1 à un point p2, l'objet doit être déplacé et tourné. Au point p1 l'objet touche la trajectoire au point q1. Au point p2 de la trajectoire, le point de contact est devenu le point q2'.
Quand un objet roule sur une trajectoire d'un point p1 à un point p2, l'objet doit être déplacé et tourné. Au point p1 l'objet touche la trajectoire au point q1. Au point p2 de la trajectoire, le point de contact est devenu le point q2'.
Si l'objet se déplace d'un point p1 vers un point p2, il nous faut calculer le nouveau point de contact q2. Ce point est déterminé par le point q1 et la distance entre les point p1 et p2. Il faut donc avoir une connaissance exacte de la longueur du contour. Pour ce faire on peut utiliser la formule suivante :
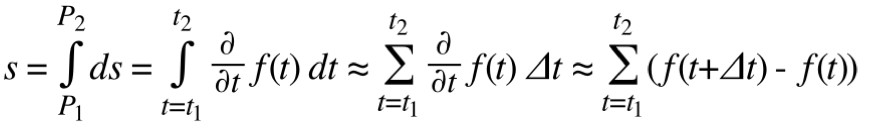 (4.1)
(4.1)
Manipulation 4.4 (optionnel) : Ajoutez à la classe MathShape une méthode computeContourLength() qui approxime la longueur du contour par la formule (4.1). Utilisez la constante Δt = 10-5.
Vérifiez votre résultat en calculant le contour du cercle avec rayon r=1 et d'une ellipse avec les demi-axes a=4 et b=2. Les résultats que vous obtenez sont respectivement 6.283 et 19.38.
Manipulation 4.5 : Créez dans la classe MathShape une méthode advance() qui retourne le paramètre t2 correspondant au point se trouvant à une distance donnée d'un point t1 lorsqu'on avance le long de la fonction génératrice. Utilisez la formule (4.1) et le prototype suivant :
virtual double advance(double t1, double length)
 La méthode
La méthode advance() nous permet de calculer à partir d'un point de contact actuel q1 et la distance entre les point de trajectoire p1 et p2 le nouveau point de contact q2. Pour faire semblant que l'objet "roule" sur la trajectoire l'objet doit être déplacé tel que le point q2 et le point p2 de la trajectoire coincïdent et l'objet doit être tourné tel que les tangentes au point q2 et au point p2 coincïdent.
Manipulation 4.6 : Ajoutez à la classe MathShape les méthodes :
PtVec getTangent(double t) qui retourne un vecteur tangent à la fonction génératrice f au point t. Approximez la tangente avec f(t+Δt)-f(t) en utilisant le même Δt comme à la manipulation 4.4.void drawTangent(double t) qui dessine la tangente au point donné par t. Cette méthode peut aider à déboguer la suite de l'étape.Conseil : Le vecteur tangent retourne par getTangent(t) doit correspondre au point retourné par computePoint(t). Alors il faut que getTangent() respecte l'orientation de la forme!
Manipulation 4.7 : Ecrivez une méthode alignWithTangentAt() qui déplace et tourne la forme (utilisez les méthodes move()/moveTo() et rotate()/setAngle()) pour que la tangente et le point donnée par le paramètre t coïncident avec le point et la tangente passé comme argument. Utilisez le prototype suivant :
void alignWithTangentAt(PtVec dst_pt, PtVec dst_tangVec, double t)
Conseil : Utilisez la fonction getTangent(t) et computePoint(t) pour calculer le point et la tangente à partir du paramètre t.
Manipulation 4.8 : La classe MathShape est maintenant complète et fournit tous ce qui est nécessaire pour implémenter la fonction principale roll(). Cette fonction parcourt la trajectoire par petits pas en "roulant" l'objet. Ceci nous permet de simuler la cycloïde et l'astroïde.
Ecrivez la fonction en traduisant le pseudo-code suivant : (=cette fonction n'appartient à aucune classe!)
void roll(MathShape &traj, MathShape &obj, int steps)
{
déterminer le domaine de définition de la trajectoire
déterminer le domaine de définition de l'objet
initialiser les paramètres t pour la trajectoire et l'objet
dessiner la trajectoire
calculer le premier point de la trajectoire
répéter pour chaque pas
déterminer la tangente au point courant de la trajectoire
aligner l'objet avec la trajectoire
dessiner l'objet (ou seulement un point de l'objet)
augmenter le paramètre t de la trajectoire d'une quantité
correspondant d'un pas.
calculer le prochain point sur la trajectoire
calculer la distance entre le point courant et le prochain
point de la trajectoire
calculer le nouveau paramètre t de l'objet qui correspond au
déplacement sur le contour de la fonction génératrice
(fonction advance())
(optionnel: faire une petite pause en utilisant usleep())
le prochain point de la trajectoire devient le point courant
fin de répétition
}
Manipulation 4.9 : Testez votre implémentation en faisant rouler un cercle de rayon 1 sur un segment de droite (=cycloïde) et ensuite sur un cercle de rayon 4 (=astroïde). Utilisez la classe LineSegment comme segment de droite :
class LineSegment : public MathShape
{
protected:
PtVec point, vec;
PtVec f(double t) { return point + (vec*t); }
public:
LineSegment(double p1_x, double p1_y,
double p2_x, double p2_y) :
MathShape(0, 1), // Parameter between 0..1
point(p1_x, p1_y),
vec(p2_x-p1_x, p2_y-p1_y) {}
virtual ~LineSegment() {}
// Draw using only 1 line (=no subdivision)
void draw() { MathShape::draw(1); }
};
Comparez le résultat avec les fonctions paramétriques Cycloid et Astroid de l'exercice précédent.
Question 4.2 : Pourquoi est-il impossible de laisser rouler le petit cercle de l'astroïde à l'extérieur du cercle trajectoire?
Si vous avez fait une bonne implémentation, vous devriez être capable de rouler un cercle sur une ellipse, ou l'inverse, ou un cercle sur une parabole, ...