3. Classe abstraite de fonctions paramétriques

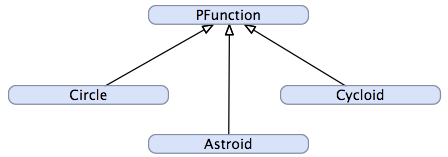
Objectif: Appliquer les connaissances de C++ acquises.

Le but de cet exercice est la création d'une classe abstraite PFunction et de ses sous-classes représentant des courbes paramétriques (données par des fonctions du type f(t) = (x(t), y(t)) qui calculent un point à partir d'un paramètre t).
Cette exercice utilise la classe PtVec qui a été mise en oeuvre lors de l'exercice précédent.

Lors de cet exercice, vous allez implémenter quatre classes: PFunction, Circle, Cycloid et Astroid. La classe PFunction est la super-classe des trois autres:
hiérarchie des classes

La classe de base: PFunction

La classe PFunction sert de classe de base dont les autres héritent. Elle réunit toutes les fonctionnalités communes aux fonctions paramétriques :

Gestion du domaine de définition du paramètre t ∈ [t_min, t_max] : setDomain() et getDomain()
Calcul d'un point spécifique de la fonction : computePoint()
Traçage du graphe de la fonction : trace()

En plus, elle déclare une fonction abstraite f :

virtual PtVec f(double t) = 0;

Explications : Le mot clé virtual assure que les méthodes surchargées par les sous-classes seront exécutées lors de l'appel à la fonction f. L'affectation = 0 déclare la fonction comme abstraite; c.-à-d. les sous-classes doivent implémenter cette fonction, sinon le compilateur ne peut pas instancier un tel objet.

Les sous-classes: Circle, Cycloid et Astroid

Ces sous-classes implémentent :

Un constructeur qui prend les arguments nécessaires pour que la fonction soit définie (par exemple le rayon du cercle) et qui initialise le domaine de définition du paramètre t.
La fonction f qui prend comme argument le paramètre t et retourne un point (c'est-à-dire un objet de la classe PtVec) calculé selon la définition de la fonction.

Les fonctions paramétriques sont définies de la manière suivante :

Circle:: x(t) = r⋅cos(t)
y(t) = r⋅sin(t)
Cycloid:: x(t) = a⋅(t − sin(t))
y(t) = a⋅(1 − cos(t))
Astroid:: x(t) = a⋅cos³(t)
y(t) = a⋅sin³(t)

Manipulation 3.1 : Créez la classe PFunction et les trois sous-classes et comparez l'affichage (produit par le programme de test) avec cette image.

Conseils:

Utilisez le programme de test ci-dessous pour tester votre implémentation.
La méthode trace() de la classe PFunction fait appel à la fonction f abstraite qui n'existera que dans les classes dérivées.
Créez deux méthodes trace(). Une qui prend comme argument le nombre de subdivisions du domaine de définition et une deuxième qui ne prend pas d'argument mais appelle la première avec un argument 100 :
void trace(int steps) { ... } void trace() { trace(100); }

Programme de test

int main(void)
{
    // Create figure window
    createWindow("Parametric functions", 901, 401);

    // Define xmin, xmax, ymin, ymax for figure window
    setAxis(-2, 7, -2, 2);

    // Instantiate circle
    Circle c(1.9);

    // Trace circle using 50 line segments
    c.trace(50);

    // Draw cycloid
    Cycloid cycl(0.5);
    cycl.trace();

    // Draw astroid
    Astroid a(1.7);
    a.trace();

    // Draw red cycloid segment
    setColor(1, 0, 0);
    cycl.setDomain(-M_PI, 0);
    cycl.trace();

    // Wait until user is ready to quit
    puts("RETURN to quit");
    fgetc(stdin);

    closeWindow();
    return 0;
}